イノベーター・ジャパン Advent Calendar 2019について

このエントリーは イノベーター・ジャパン Advent Calendar 2019 の1日目の記事です。

こんにちは、イノベーター・ジャパン人事の菊池です。早いものでこの12月で入社9ヶ月目となりました。その短い間にも、IJには大きな変化があったと思います。

一つは顧客ビジネス変革ヘ向けた高付加価値化・海外展開の動き。Digital Transformationを掲げ、主力ソリューション群「Media DX」と、その中核プロダクトである「Open Media Suite」をリリースすることができました。海外展開構想、インド企業との協業なども活発に動き始めました。

さらに、IJが目指したい「人間的な価値をどう実現するのか」という経営理念の話題も増えました。

ざっと思い起こすだけでも、新経営理念「Human Well-Being」を受けた新ロゴの発表、「アート思考」リサーチインターンプログラム実施、デンマーク大使館投資部共催「北欧式イノベーション創発戦略マスタークラス」実施などなど、イノベーションを生み出す人間の力の源泉を探ろうという動きが活発になった年と言えるかと思います。新経営理念と新事業が融合するには時間がかかりますし、会社・社員も色々な方向に変化（Transformation）していくことになるでしょう。

そこで、今年のAdvent Calendarのテーマは自分に起きた変化を振り返ってみようということで「Self-Transformation」となりました。

ArtとBusinessをつなぐTech

私個人についていえば、今年は幸運にも偶然が重なり、一つのテーマとなって動き出した変化の年といえます（もちろんIJ入社も含めて！）

1) Pythonを使ったモデリングに取り組み始めたこと

4月頃から趣味でPythonを使って市場価格予測のWebアプリを作ろうとしていましたが（長くなるので機会があれば）、途中から予測技法としての自然現象のモデル化にも関心を持つようになりました。その中で、昔興味はあったけれど理解しきれなかった複雑系やカオスの本を改めて読むようになっていました。

2) 「アート思考」リサーチインターンプログラム実施

インターンの安藤さんに2週間取り組んでいただき、「異なる文脈をつなぐことの重要性」とその手段としての「アート」概念 を整理してもらいました。もともと 社内では自然の原理をビジネスに活かせないか？ という問題意識があったのですが、その媒介としてアートがあるのではないか、という形でよりクリアになっていったと思います。

ただ、アートや自然の原理がなぜビジネスに活きるのか？その論理はまだまだブラックボックスなのではないでしょうか。これを活かす方法として「直感力」「美意識」などに還元してしまうのは、個人的には具体的イメージが持てないのです。そこで、何らか自然模倣のモデリングを噛ませることによって、「美的」な要素は維持しつつ、操作性を持たせて、現実への応用が可能になるのではないか？ と思っています。今回そのモデリングの方法として、複雑系やカオスに触れてみることにしました。

レスラー方程式をSciPyで描いて遊ぶ

※専門家ではないため高度な内容は数学の書籍に譲ります...！

「一定の規則に従って時間の経過とともに状態が変化するシステム（系）、あるいはそのシステムを記述するための数学的なモデル」（Wiki） のことを力学系といいます。まさにビジネスとか経済も時間を通じて変わっていくため、一種の力学系と捉えることができます。力学系の中には、時間を通じた生物の捕食・被食の変化を描写するLotka-Volterra方程式など生物学に応用されているものもあります。

力学系の中でも、初期値やパラメータがほんの少し違うだけでモデルの振る舞いが大きく変わってしまうため、事実上（長期の）予測ができないものをカオスと呼びます。今回はそれと関連するリミットサイクルを取り上げます。経済・ビジネスへの応用を考えるため、空気の対流を理論研究用に簡略化したという 「レスラー方程式」 と Pythonの数値解析パッケージ「SciPy」 を使い、企業行動の変化を描いて遊んでみたいと思います。

モデルとコード

レスラー方程式は、この３つの微分方程式で書くことができます。ビジネス用語を当てはめ、v = 利益, u = 費用, k = 投資として、各式は下記のような意味合いを持たせてみます。a,b,cは適当に決めるパラメータです。

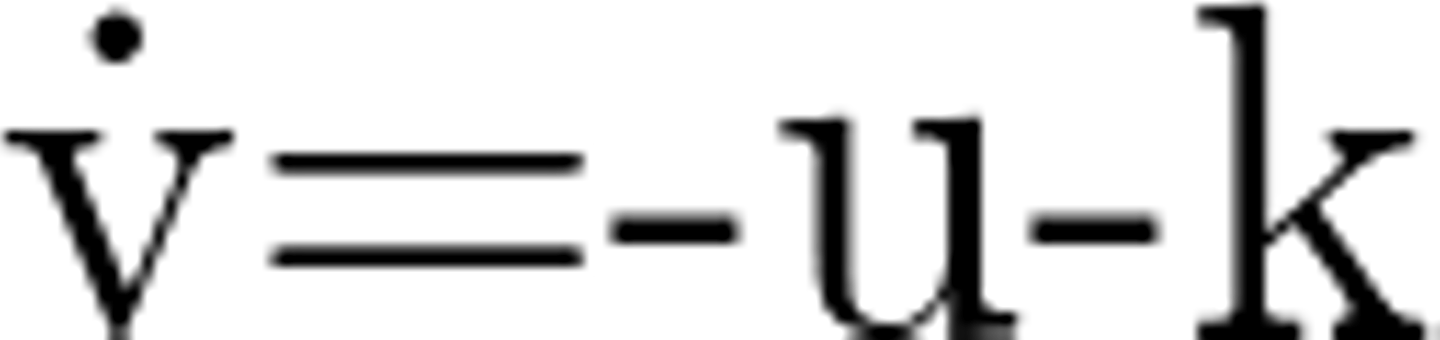
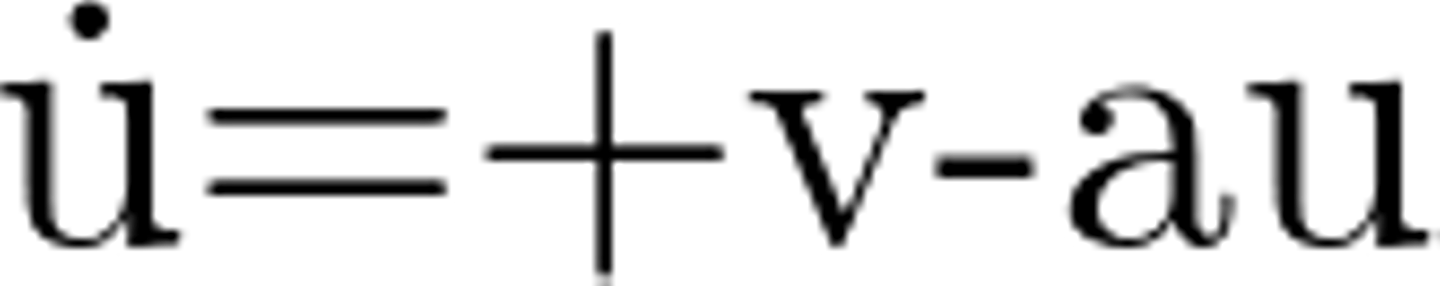
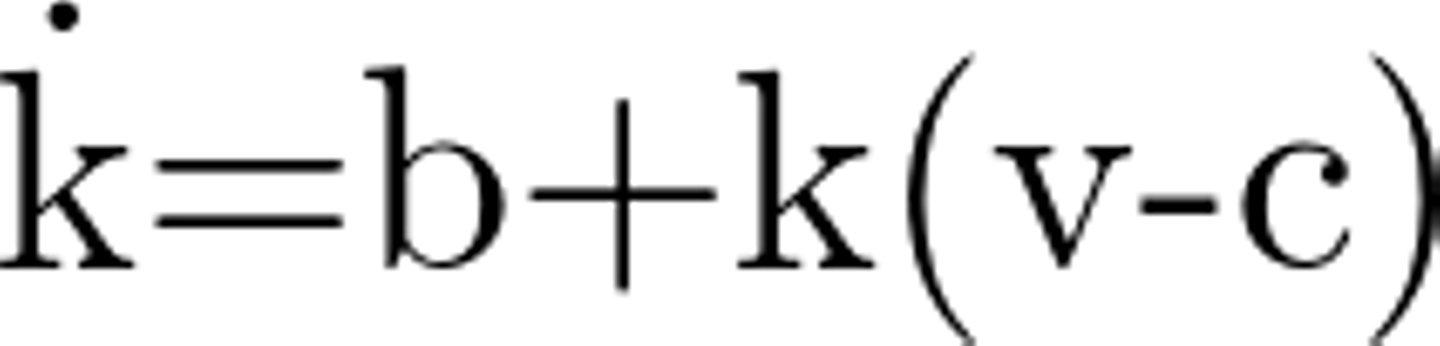
- v ... 次期利益は費用と投資が増加すると減る
- u ... 次期費用は今期利益が増えると増加（事業拡大）、今期費用が増えると減少（節約）
- k ... 次期投資は、今期投資に今期利益の一部を掛け合わせた部分で実施

import numpy as np
from scipy.integrate import odeint #微分方程式を解く関数を呼び出す
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 初期値
# v = 利益, u = 費用, k = 投資
# x0[0]がv(0), x0[1]がu(0), x0[2]がk(0)
x0=[3.5,4,0]

# レスラー方程式
def eq(x,t,a,b,c):
    return [-x[1]-x[2],x[0]+a*x[1],b+x[2]*(x[0]-c)]

# パラメータ
a, b, c = 0.2, 0.2, 3.1

# odeintを使って方程式を解く
t=np.arange(0,100,0.01)
x=odeint(eq,x0,t,args=(a,b,c))

# 描画
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(x[:,0],x[:,1],x[:,2])

ax.set_xlabel("$v$")
ax.set_ylabel("$u$")
ax.set_zlabel("$k$")
ax.set_xlim(10, -10)
ax.set_ylim(-10, 10)
ax.set_zlim(0, 20)
plt.title("a={0},b={1},c={2},v(0)={3},u(0)={4},k(0)={5}".format(a,b,c,x0[0],x0[1],x0[2]))
plt.show()

結果

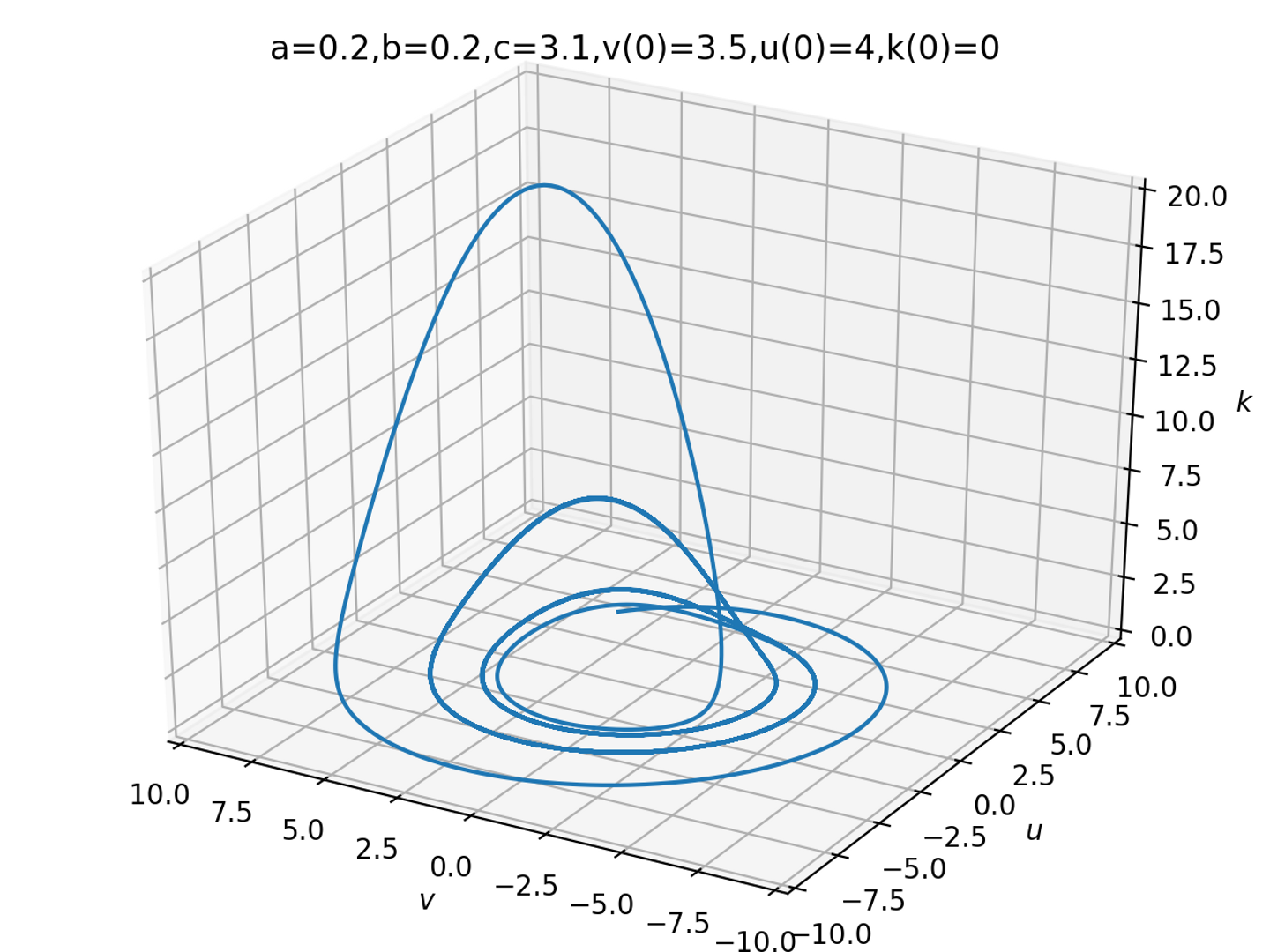
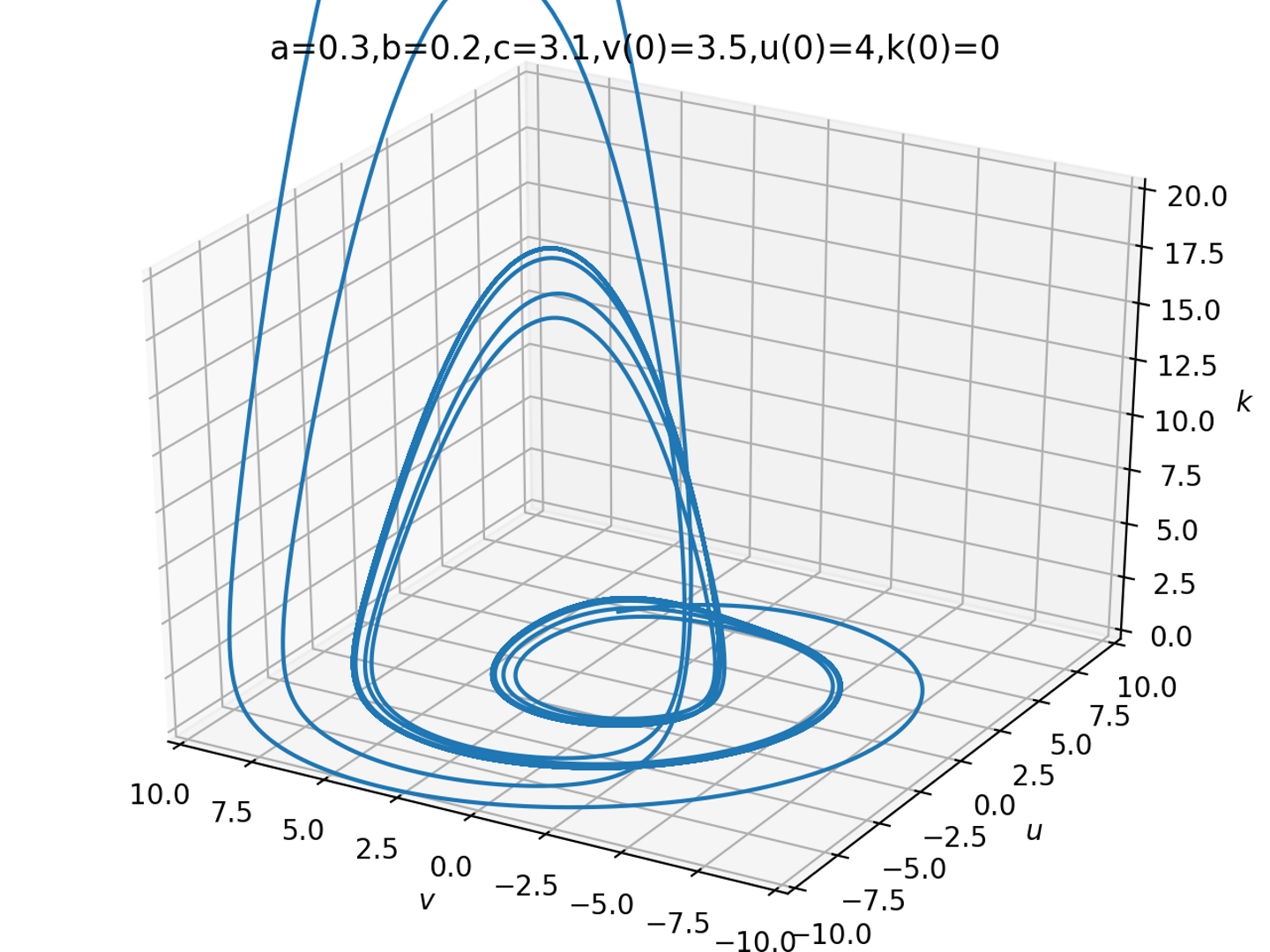
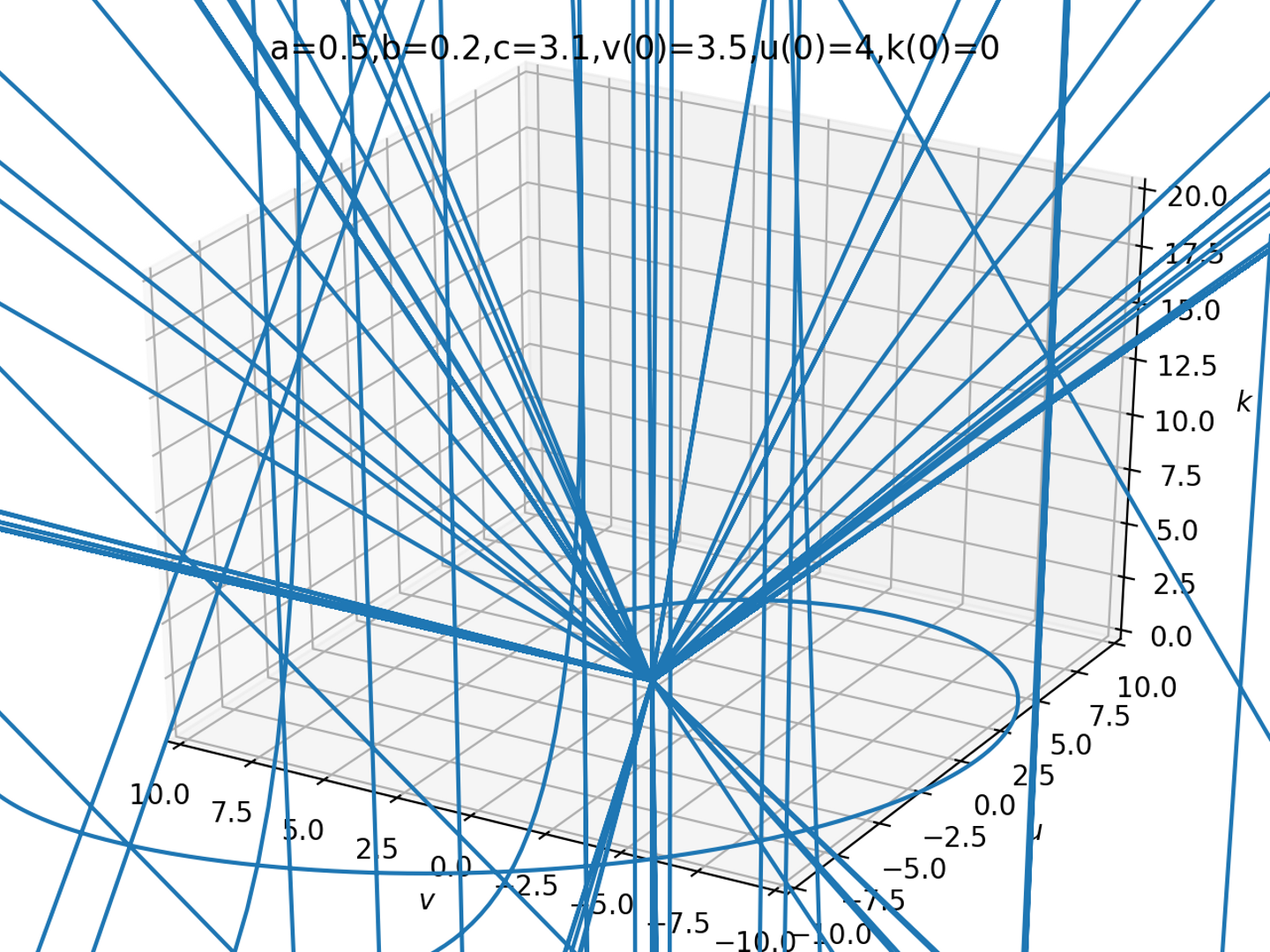
利益vと費用uが最初のうちは増減を繰り返しているのですが、利益が増えてくると急にkが増えて投資が始まり、投資が増えすぎるとまたコスト面で圧迫されていく様子がみられます。ちょっとパラメータを間違うと、どこかへ行ってしまったりします。全く違う図が描けるのが面白いですね！

今回はちょっと式を使って遊んでみただけですが、イノベーションを導入したり、別の方程式を使ったり、本当に面白い分野であると感じています。いつか組織論にも応用できないか、チャレンジしてみたいと思います。

参考文献

• R.M.グッドウィン「カオス経済動学」（1992、多賀出版）
• Steven H. Strogatz「ストロガッツ 非線形ダイナミクスとカオス」（2015、丸善出版）
• ジャルヴァース・R・ブッシュ他「対話型組織開発――その理論的系譜と実践」（2018、英治出版）