自己紹介
こんにちは。
ProsConsでリサーチインターンをしている東京大学工学部のたじまです。
会社のベンチマーキング業務体験の一環として、特に異常検知手法の一つとして用いられるVAEに関する記事を書かせていただくこととなりました。
よろしくおねがいします!
本記事はQiita(https://qiita.com/maharuda/items/9e9ef8ab021a2cb18573)にも掲載しております。
背景と目的
深層距離学習、生成モデルを用いた様々な異常検知手法が提案されています。
その中でも2018年度人工知能学会全国大会で発表された、複雑な工業製品をVAEで異常検知する際に有用な非正則化項を用いた異常検知手法を用いて実験しました。
その手法の中で正常な部分に誤って異常判定が起きる問題、具体的には標準偏差出力層σが過少に評価されることによる過大な異常判定が生じる問題があり、その解決手法を検討しました。
今回は、データ拡張による精度向上効果を検証します。
(データ拡張とは…画像に変換処理(反転、拡大、縮小など)を加えることで、学習データの「水増し」を行う。水増しされることで同じ画像が学習されることが少なくなるので汎化性能が改善される。)
非正則化項を用いた異常検知手法で実験している際に生じた問題点の一つ、正常部分の誤った異常判定を改善します。
VAEを用いた異常検知
データXを潜在変数z(元データより次元が少ない)に変換するニューラルネットワークをエンコーダー、潜在変数zを再構成して元のデータを復元するニューラルネットワークをデコーダーと呼びます。入力データと再構成されたデータがなるべく同じになるように学習させます。
以上のアーキテクチャをオートエンコーダー(AE)と呼びます。
そしてAEの潜在変数を確率分布に押し込めたものをVAEと呼びます。
以下の記事で詳しく解説されているので参考にしてください。
・Variational Autoencoder徹底解説
(https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24)
一般的に、VAEを用いる異常検知は、エンコーダーに入れる前のデータとそれをVAEで再構成したデータとの差分を異常として検知することにより実現します。
複雑な工業製品の異常検知に有用な手法
工業製品は様々な要素から構成されています。
例えば歯車でいうと歯車の平らな表面、歯の部分や中心の穴などからです。
頻繁に出る画像要素は尤度がたまにしか出ない画像要素よりも高くなります。
そのため損失関数を異常検知の関数として用いると頻繁にでる画像の異常とみなす閾値はたまにしかでない画像のそれよりも大きくなります(頻繁に出る画像においては異常部分もたまにしか出ない画像における異常部分よりも頻繁に出る、ということです)。
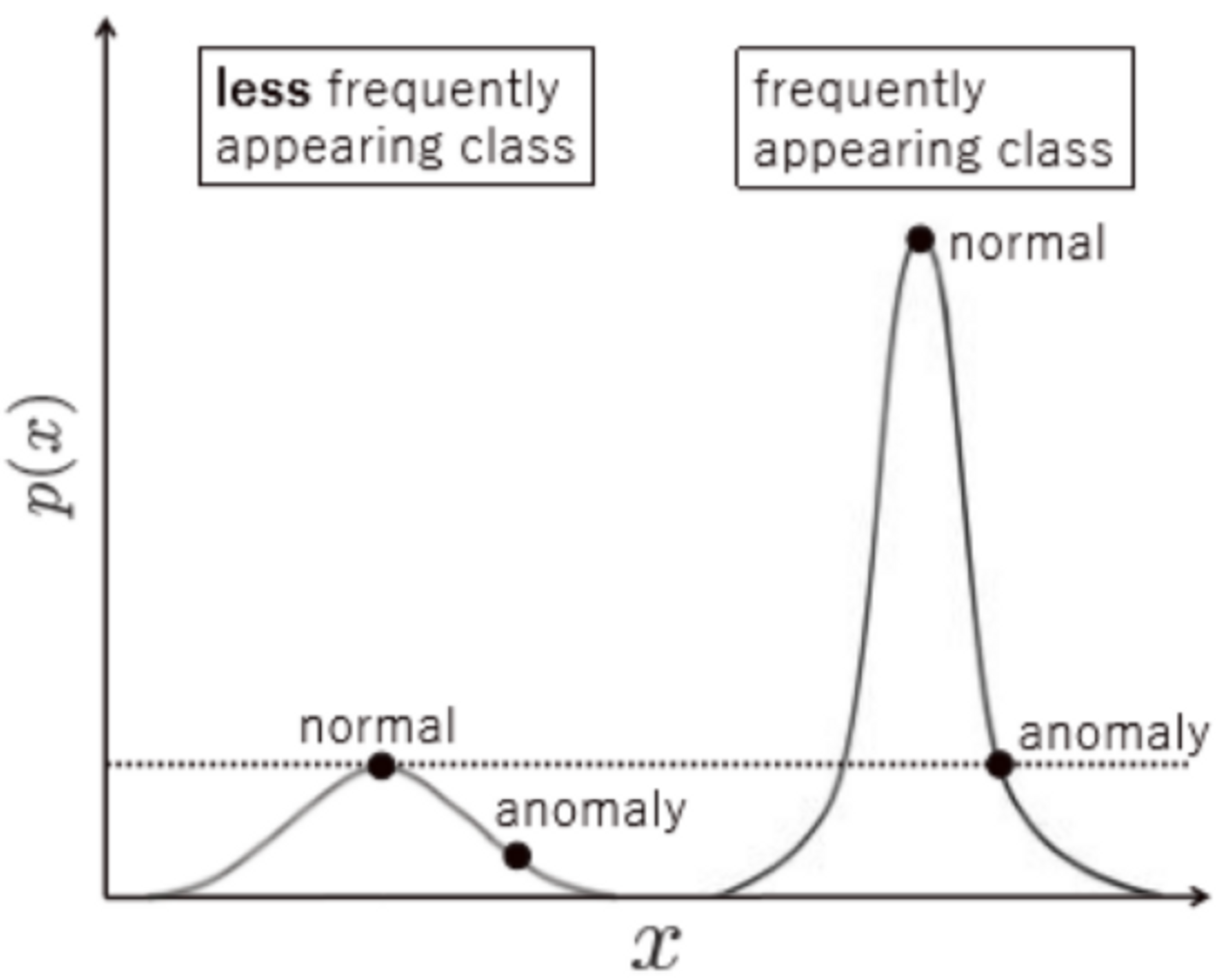
図1.工業製品画像における尤度の直感的な図解(論文より)
以下の論文で画像が属するグループの複雑さや頻度の影響を除去できる手法が提案されています。
これを用いると複雑な工業製品(単純な部分にも異常がでるような対象物)の画像に対して異常検知をすることができます。
・深層生成モデルによる非正規化異常度を用いた工業製品の異常検知
(https://confit.atlas.jp/guide/event-img/jsai2018/2A1-03/public/pdf?type=in)
VAEの損失関数は
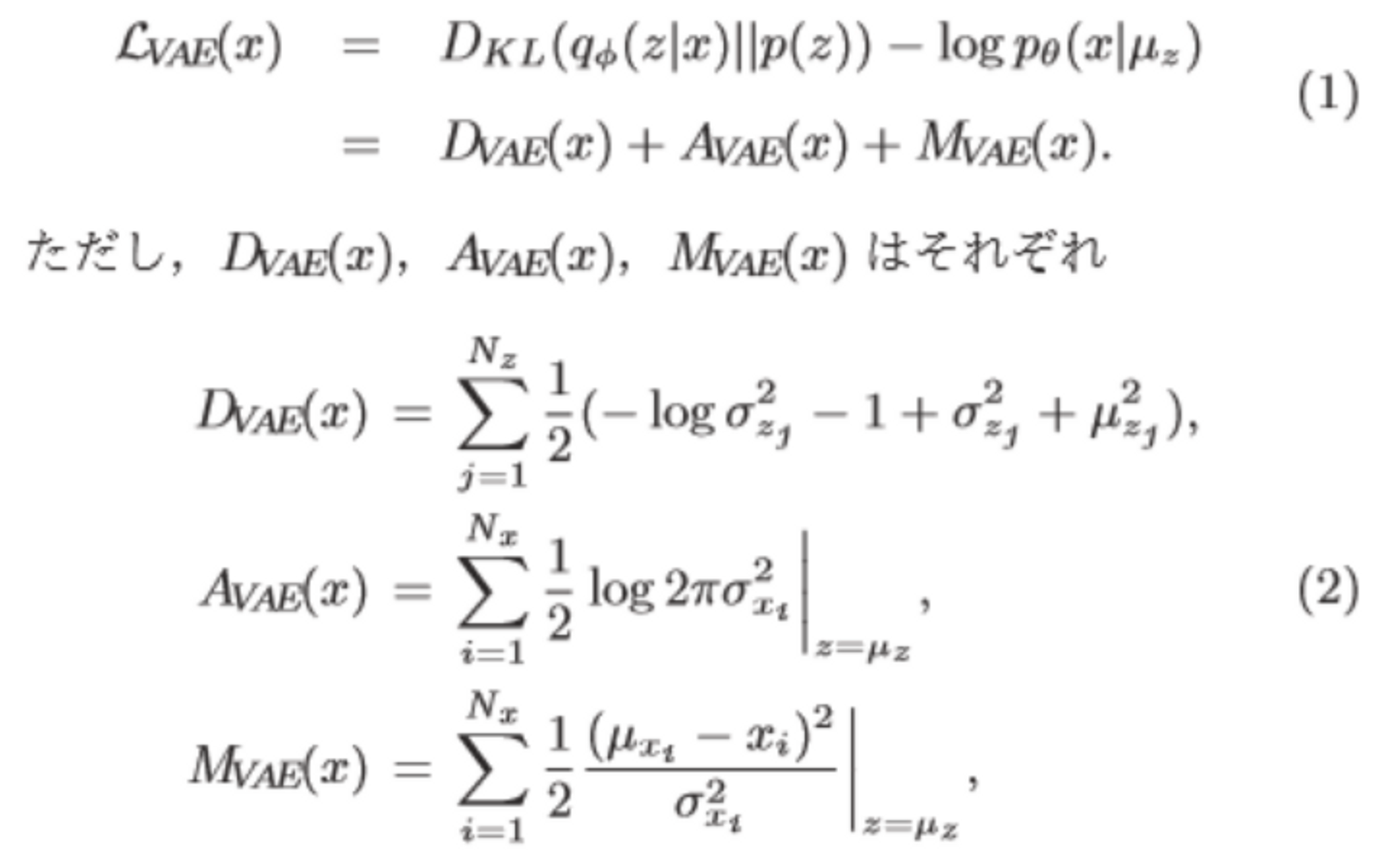
で表せます。(論文より)
一般的にはVAEの異常検知の評価にこの損失関数L_VAEを用いるのですが、
L_VAEからD_VAEとA_VAEを差し引いたM_VAEとすることで同じ閾値で異常判定できるように改良しています。
M_VAEはデータxの平均とデータxの差分の二乗を分子に持ち、潜在的にデータxの不確かさや複雑さを表している標準偏差σxを分母に持つ関数です。
後述しますがこのM_VAEの分母にあるσxが小さすぎることで問題を引き起こします。
この論文で取り上げられている手法は以下の記事で詳しく解説されているので参考にしてください。
・Variational Autoencoderを使った画像の異常検知 前編
(https://qiita.com/shinmura0/items/811d01384e20bfd1e035)
早速この手法を用いて異常検知をしてみましょう。
検証結果
小さな白い歯車を異常検知の対象として用いました。
結果の画像は左から
・異常部分をヒートマップで表した画像
・元画像
です。
<正常画像>

<異常あり画像1>
異常:右側の歯が欠けている

<異常あり画像2>
異常:すべての歯が摩耗している

異常な部分(歯車の歯が欠けている部分)を検出してくれていますが、
正常な部分(白い歯車の表面)にも異常判定がでてしまっています。
仮説
VAEでは、再構成の不確かさに関して標準偏差σxが調整されることにより、A_VAEとM_VAEのバランスが取れるように学習が行われる。(論文より)
とあるように損失関数を減らす方向に学習は進むため学習時にM_VAEが大きな状態であるとは考えにくいです。
学習時は平均ベクトルμxがx限りなく近づいており、σxσxが非常に小さな値でもM_VAEを小さく抑えることができており、そのため異常検出時に(μx−x)^2が少しでも大きくなるとM_VAEが跳ね上がってしまうと考えられます。
以下で解決策を模索していきます。
解決策(データの拡張)
損失関数を下げようとする方向に学習は進みます。
一方でデータが水増しされたことで学習時にμxとxが近づきにくくなります。
そうすることでσxが小さくなりすぎるのを防ごうと思います。
パターン1
もとの画像の各ピクセルのRGBの値をそれぞれ2(4,6,8,10)下げた画像をデータに加えます。
データの量は6倍になります。
加工前の画像 RGBそれぞれから10差し引いた画像

<正常画像>

<異常あり画像1>
異常:右側の歯が欠けている

<異常あり画像2>
異常:すべての歯が摩耗している

うーん。誤って異常判定しています。
パターン2
俗に言うソルトペッパーノイズをいれました。
白点と黒点の比は1:1にしました。
加工前の画像 ノイズの比率0.4%

<正常画像>

<異常あり画像1>
異常:右側の歯が欠けている

<異常あり画像2>
異常:すべての歯が摩耗している

割といい感じ。
完全に除去とまではいきませんが正常な部分にかかっていたヒートマップが少なくなっていますね。
仮説
パターン2については良い方向に結果がでており、データを拡張することでデータに多様性が生じて、μとxに差分がうまれてσが小さくなりすぎないことがわかりました。
正常部分を誤って異常判定するこの問題に対するデータ拡張の有用性が示されました。
またパターン1では精度向上しなかったことを踏まえ、データ拡張の中でも有用と言える場合と言えない場合があることがわかりました。
今回行った検証実験に関しては、均一にRGBを下げるよりも部分的に白(0,0,0)もしくは黒(255,255,255)のピクセルを設ける方が異なる画像としてうまく特徴量を抽出でき過学習を防ぐことができたと言えます。
したがって明暗を変更した画像の拡張は形状情報に関与せず、本質的な複雑さに影響をあたえておらず、対してソルトペッパーノイズの画像の拡張は形状情報を変更しており本質的な複雑さが増えているために有効に働いたと考えられます。
よって、これに関しては仮説段階ですが、形状情報を変更した画像の方がデータ拡張に有用である可能性があります。
結論として、データ拡張は非正則化項を用いた異常検知手法における標準偏差出力層σの過小評価を防ぐことができる。データ拡張に形状情報が変更された画像を用いるか否かが有効性に関与している可能性がある。ということが言えると思われます。
インターンを終えて
一ヶ月という短い期間にもかかわらず機械学習に関して深くまで学ぶことができました。
Pros ConsではGemini eyeという、工業製品の外観検査AIを開発しています。そのベンチマーキング業務という形で業務に携わらせていただき、非常に有意義な経験でした。居心地のよい会社で働かせていただきありがとうございました。
/assets/images/3890528/original/ae3b9697-3815-4bbb-b5c0-f84c1da3dfde?1562141623)

/assets/images/3890528/original/ae3b9697-3815-4bbb-b5c0-f84c1da3dfde?1562141623)


/assets/images/3890528/original/ae3b9697-3815-4bbb-b5c0-f84c1da3dfde?1562141623)

/assets/images/3890528/original/ae3b9697-3815-4bbb-b5c0-f84c1da3dfde?1562141623)
