データサイエンスチームリードの中橋です。 前回の記事で、我々JDSCでは現実の制約や先験的知識などドメインの情報を組み込んだモデリングに挑戦していることを紹介しました。そのためのアプローチの1つとしてベイズモデリングを挙げたのですが、今回は具体的な例を取り上げながら紹介してみたいと思います。
問題設定
製造業のデータ分析に関わっていると、次のような相談を受けることがあります: 「不具合が1件だけ出ているのですが、これが今後増えるかわかりますか?」
これは大変むずかしい質問です。収集したデータからパターンを見つけていくという統計学や機械学習の立場からすると、「この状況では何も言えません。あえて言うなら不具合の発生確率は少なくとも0ではない、ぐらいです」というのが教科書的な意味で正しい・誠実な回答となるでしょう。
一方で特に品質保証の部門が一番知りたいのは正にこのような 不具合が1件しか発生していない状況における将来的な見通し です。この不具合が発生したのは偶然なのか、それとも設計・製造に起因するものであるのか。これから不具合が増加するのか、するとしたらどの程度か。こうした疑問に答えて意思決定を進めていくために、現場では「情報が少ない中でも判断するための枠組み」が求められます。
JDSCはこのような場面における意思決定を支援するためのアプローチを考えています。本記事では不具合の発生件数の分析でよく利用されるワイブル解析をベースとし、最初に「N=1ではパラメータの推定はできない」という原理的な限界を確認したうえで、それでも実務で議論を進めるための方法を検討します。その鍵になるのが、事前知識をどう扱うかという点です。
ワイブル解析
市場での不具合について分析する際、よく使われるのがワイブル分布です。ワイブル分布は2つ(または3つ)のパラメータによって不具合の発生が時間とともに増える・減るといった挙動を柔軟に表現でき、確率密度関数は次の形となります:
ここで k(>0)・λ(>0) はそれぞれ形状(shape)・尺度(scale)パラメータです。ワイブル分布は初期故障や経時的な摩耗による故障など製造業における代表的な不具合の発生パターンを表現できることから、ワイブル確率プロットなどで推定した shape や scale から故障モードを考察したり、また故障モードが変化するタイミングを評価することが可能[1]です。
[1]…実際には複数のモード・パラメータのワイブル分布が混合していることも多く、慎重に解釈する必要があります https://www.jstage.jst.go.jp/article/reajshinrai/42/3/42_102/_pdf

N=1となるケースでの問題
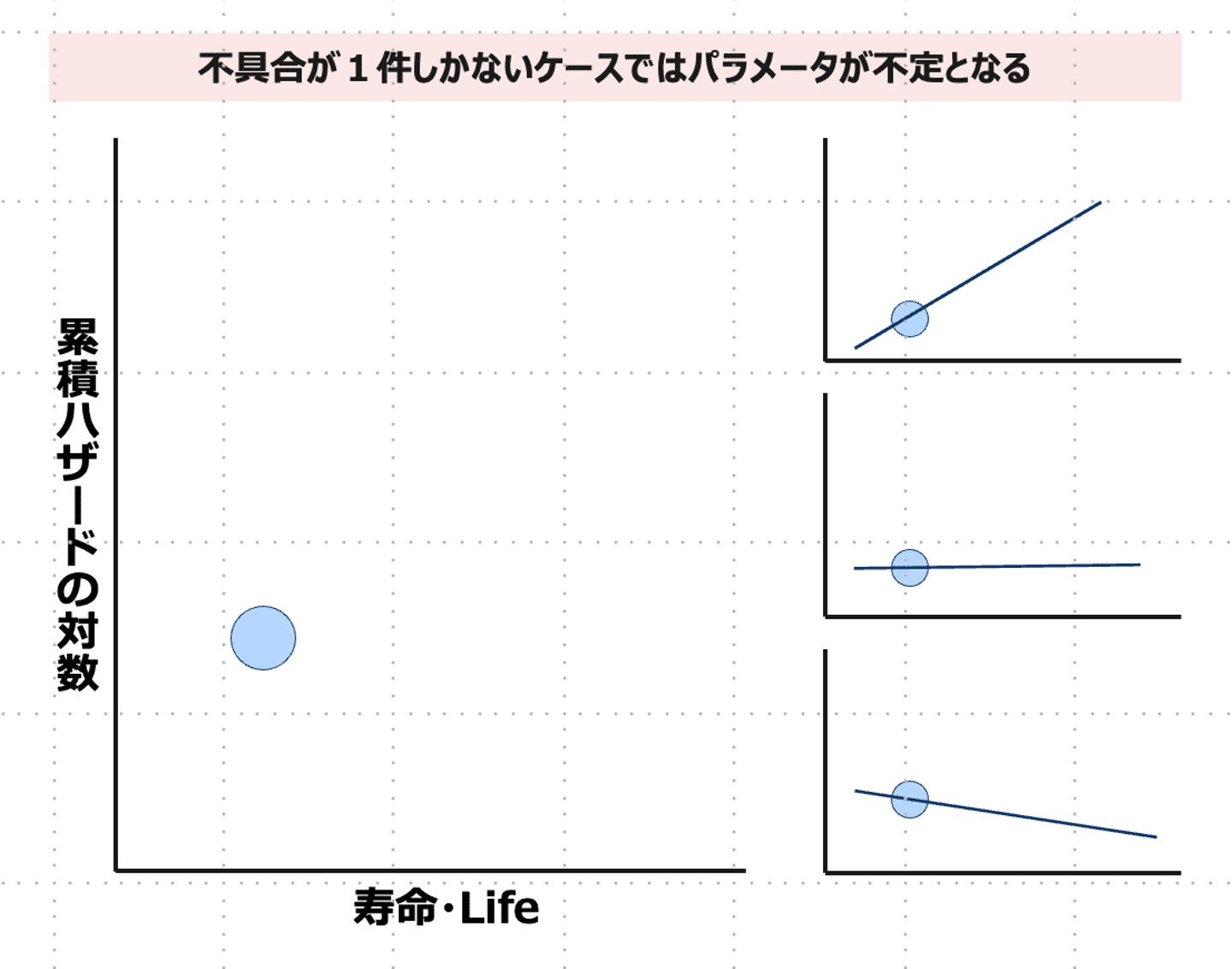
不具合の発生がワイブル分布にしたがう場合、十分なデータがあれば上記の手順で妥当な推定が可能です。一方で、問題設定の節で紹介したような「不具合が1件しか発生していない状況」ではこの手順が成立しません。というのもワイブル確率プロットは線形回帰により推定したパラメータをもとに shape/scale を求めますが、不具合が1件しかないケースでは shape / scale が一意に定まらないためです。
では、それでも何らかの判断を行いたいときにどのような方法が考えられるでしょうか。我々はベイズ化による事前知識の取り込みが1つのアプローチであると考えています。
事前知識の取り込み
ある製品において何かの不具合、たとえば特定の部品における設計や加工不良による異音や振動などが確認されたとき、製品の担当者は該当部品の不具合 だけ を気にするでしょうか。きっとそうではなく、例えば
- この部品を利用している他の製品ではどうだろうか
- このサプライヤーに加工を依頼している他の部品は大丈夫か
- この部品を組み込んだアッシの他の部品はどうか
などを考えるでしょう。このような現場の担当者の思考をモデルに組み込むためのアプローチとしてベイズモデリングがあります。
ベイズモデリングとは、ベイズの定理を基盤とした分析・モデリング手法のことです。ここでベイズの定理とは以下の式を指し、事前分布と標本モデルによって事後分布がどのように変化するかを定めたものです:
ここで注目したいのは p(θ) で、これはパラメータ(ワイブル分布であれば shape や scale)自体に対する分布(信念)を表しています。ワイブル分布のパラメータ、例えば shape(k) において値が1未満であれば初期に不具合が集中する初期故障型であると解釈されますが、この shape の事前分布として1よりも低い値にピークを持つような分布、たとえば
を設定することで「この不具合は初期故障型であろう」という信念を表現することになります。実際には新たな不具合を観測するたびに事後分布が更新されるため、例えば一定期間が経過してもなお不具合が発生するようであれば「初期故障型である」という信念は徐々にデータによって覆されていくことになりますが、データが蓄積されないうちはこの信念が強く反映されることとなります。
ということは、shape や scale に対する事前分布を適切に設計できれば、少数(極端にはN=1)の不具合に対して何かしらの言及が可能になりそうです。「適切に」というのがポイントで、「どうせデータが収集されれば補正されるから何でも良い」というわけにはいきません。でも具体的にどうすればよいでしょうか?
ここで上記のような「現場の担当者が気にしていること」をもう一度思い出してみましょう。例えば、同一のサプライヤーで過去に初期の不具合が続いた、設計起因で不具合の発生が早まっている、あるいは特定の加工工程に偏りがある、などといった知見は経験則として現場に蓄積されていますが、それらの「現場感覚」を事前分布という形で表現できればモデルの中に明示的に反映することができるのです。例えば
- 同一のサプライヤーで過去に初期の不具合が続いた → shape を1未満に寄せる
- 設計起因で不具合の発生が早まっている → scale を小さくする
などが考えられますが、このように 現場の担当者が普段から注意しているポイントを p(θ) の設計として言語化できれば、彼らの経験則をモデルの中に取り込むことができるのです! そうすることで、N=1 のようなデータが乏しい状況でも、どの程度リスクが高そうかを議論できる形になります。
おわりに
本記事では、前回紹介した「先験的な知識をモデルに組み込む」というアプローチについてより具体的に紹介しました。ただし、こうした現場の感覚をモデルに取り込むためには現場の業務や制約への理解と、数理モデルが何を表現しうるかという理解の両方が欠かせません。モデルという抽象的な表現と、現場という具体的な事象を行き来しながら、どの知識をどのパラメータにどう反映させるかを丁寧に設計する必要があります。
我々は今後もモデリングの技術を磨き続け、実用性の高い分析を提供していきたいと考えています。
JDSCのデータサイエンティストに興味のある方はこちら

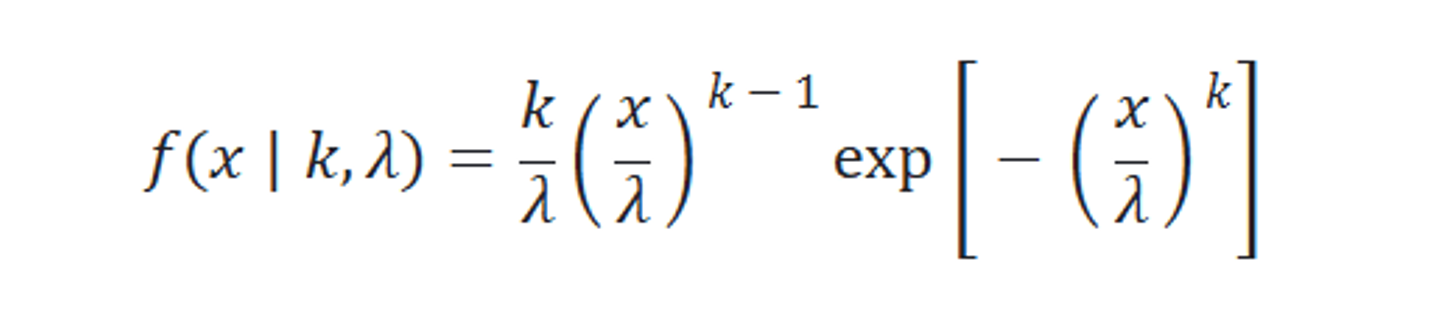
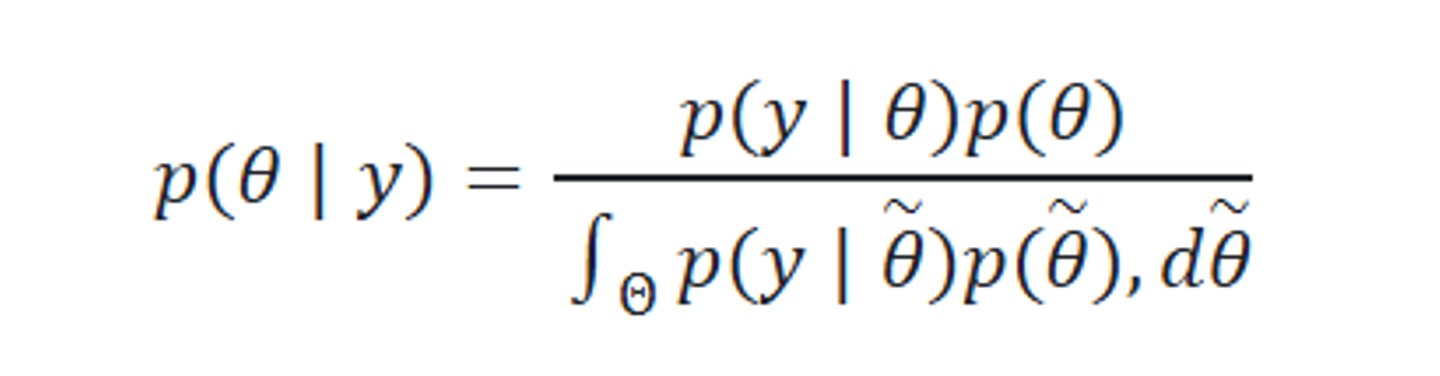
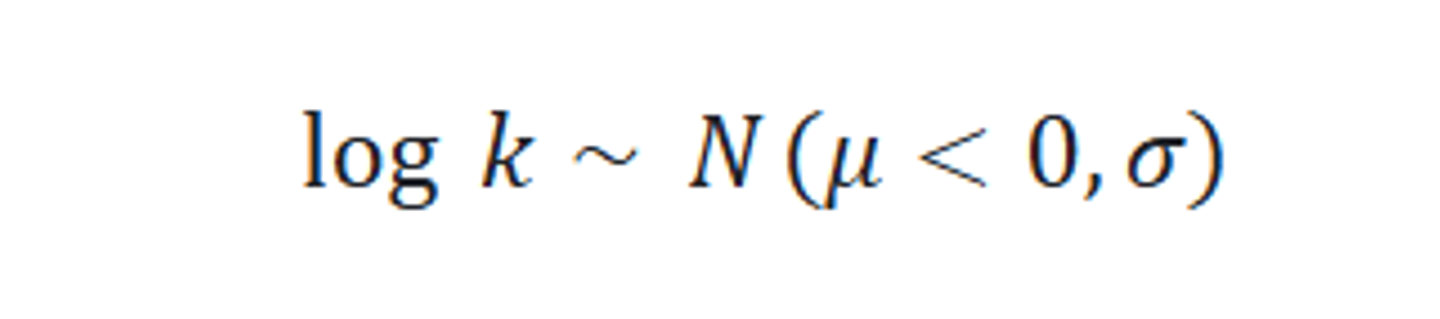


/assets/images/4569784/original/46f965d4-cc8c-4344-a2ce-9b004b3b9cb5?1580797425)


/assets/images/4569784/original/46f965d4-cc8c-4344-a2ce-9b004b3b9cb5?1580797425)
/assets/images/4569784/original/46f965d4-cc8c-4344-a2ce-9b004b3b9cb5?1580797425)