「そろそろアレ買わないとなぁ」

ｽﾏﾎﾁﾗｯ

「絶妙なタイミングでアプリの通知が来てる……こわっ……でもポチッちゃう……」

ﾎﾟﾁｰ

場面は変わって、その1ヶ月前、"アレ"を販売する企業のEC（通販）マーケティング部にて・・・

「"アレ"、売れ行きは好調なんだけど、今一歩ターゲットにしてるお客さんに刺さりきってない感じがあるんだよなぁ」

「原因はいろいろありそうだけど、通知のタイミングが悪いから埋もれちゃって、うちが"アレ"を売り出したことを知ってもらえていないとかあるかもしれない」

「同じ時間に一斉通知するのはやめて、気味悪がられるかもしれないけど、一人ひとりスマホを見そうなタイミングに通知を飛ばしたい！できれば通知飛ばすべき時間とかも自動分類したい！」

「よし。決定木に相談だ！」

「いや、軽くデータを調べる分にはいいけど、自動分類とかまでしたいなら決定木だと精度出ないよ」

「え、なんで？というか、そもそも精度の良し悪しってどう考えるんだ・・・？」

カスタマーリングス事業部で開発をやっています。油山です。

というわけでこの記事は、マーケティングの分析・予測の手法として、決定木とその派生手法について4回に渡って紹介する記事のその3です。

今回は、機械学習の良し悪しを測る概念と、実践的にもよく用いられている決定木の派生手法をさらっと紹介します。

1. 気味悪いくらいピッタリなタイミングで飛んでくる通知の裏側には健気に木を植え続けるマーケターの姿があった
2. 気味悪いくらいピッタリなタイミングで飛んでくる通知の裏側には健気に木を植え続けるマーケターの姿があった ～育った木はどんな姿をしているか～
3. 気味悪いくらいピッタリなタイミングで飛んでくる通知の裏側には健気に木を植え続けるマーケターの姿があった ～育った木の良し悪しを測ってみる～ ←イマココ
4. 気味悪いくらいピッタリなタイミングで飛んでくる通知の裏側には健気に木を植え続けるマーケターの姿があった ～精度を上げるには森を作るしかない～

図1: マーケターが木を植えた結果、色々上手くいく様子を表した図

この一連の記事は決定木について、「どこでどう使うのか」「結果はどう解釈できるのか」「実践的にはどう使われているのか」を紹介するもので、次の内容から構成されます。

• マーケターの仕事は「分類」が肝心で、それを楽にする手段の1つとして決定木を紹介（第1回）
• 決定木は機械学習モデルの1つ。よくわからないのでさらっと機械学習を紹介（第1回）
• 例を交えつつ、決定木とは実際に何をしてくれて、どうやって使うのかを紹介（第2回）
• 悪い決定木の問題点を調べ、汎化性能という機械学習モデルの良し悪しを測るものさしを紹介（第3回）
• 決定木は1本単体で使うだけでは、その汎化性能に致命的な弱点があることを紹介（第4回）
• それを克服する、GBDTとランダムフォレストという決定木をたくさん用いる手法をさっと軽く紹介（第4回）

弊社のカスタマーリングスでも実際に、メールなどの配信の際に最も開封・既読されやすいタイミングを顧客1人1人に対して予測して、この記事のタイトルのような気味悪いけれどなんだかんだ嬉しいことをする機能などに、決定木の派生手法であるGBDTが応用されています。

前回（第2回）の記事はこんな内容でした

• 都合のいいデータをもとに、通知を飛ばすべき時刻を予測する決定木を作って（チューニングして）みた。
• 決定木はデータさえあればツールで簡単に作れる。
• 決定木は機械学習のモデルの1つで、結果の解釈がしやすい。特徴量が多ければ、作った決定木を見ることで、初めて得られる気づきがあることも。
• 決定木はあまり深く作りすぎるとよくない。（なぜよくないかはこの記事で）
• データが少なくて、特徴量が尖っているとよくない。（なぜよくないかはこの記事で）
• 通知を飛ばすべき時刻を予測する決定木の例を、機械学習の流れに当てはめてみた。

今回はこんな内容です

• 深すぎる決定木や、少ないデータから作られた決定木は何が良くないのかということを調べる。
• データは、[全体の平均] + [個体差] + [ノイズ] という形に分解できることを確認する。
• モデルの良し悪しは、汎化性能というものさしで測られることを確認する。
• 過学習という、学習に用いたデータに偏り過ぎて汎化性能が落ちる現象を確認する。

いい決定木と悪い決定木

前回の記事では、都合のいいサンプルデータに対して、決定木の具体例を3つ作りました。

改めて、決定木とは、未知のデータをいい感じに自動分類するためのツールで、サンプルデータ（教師データと呼ばれる）を基に学習（チューニング）させることで使えるようになるものだとここでは思ってください。

1. 商品ページを表示した時刻を予測するざっくりした決定木
2. 商品ページを表示した時刻を予測する細かすぎる決定木
3. ドラえもん世界の性別を分類する決定木

このうち、1つ目の決定木は「結果の見た目的に、感覚的にも違和感ない分類ができると言えそうだ」というそれっぽいものになりましたが、一方で、2つ目と3つ目の決定木は「自動分類器」としてはなんとなくポンコツっぽいという結論になりました。

では、2つ目と3つ目の決定木はなにがまずいのでしょうか。

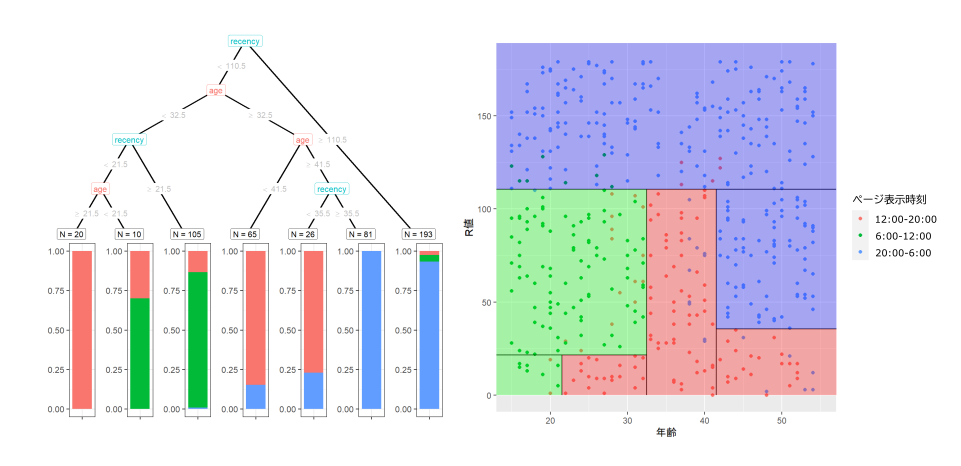
図2: 前回の記事で作成した1つ目の決定木。年齢とR値という2つの軸により、個々の顧客がいつ頃商品ページを見ているかを「いい感じ」に分類する。（※これはいい決定木の例です）

細かすぎる決定木は、教師データに振り回され過ぎるのでポンコツ

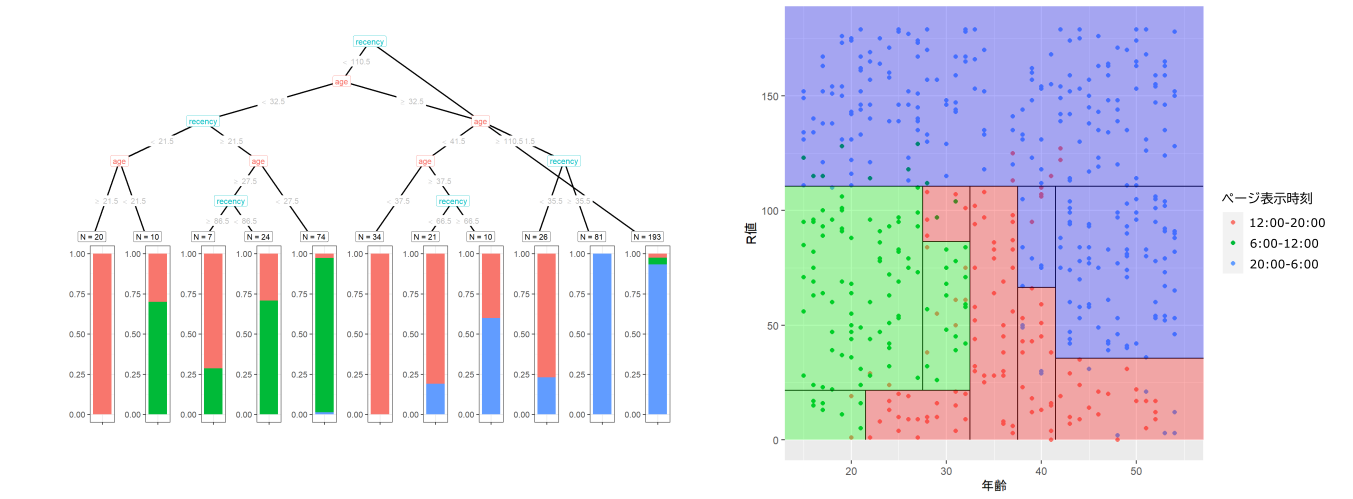
図3: 前回の記事で作成した2つ目の決定木。1つ目の決定木より細かく分類する。この複雑さにより、教師データにはよりフィットする。が、教師データ以外に対してはどうだろうか。

細かすぎる決定木は基本的にポンコツと言っていいです。それはなぜかということを考えます。

決定木はデータを分類するためのモデルですが、そもそもデータは何から構成されるのでしょう。

データ分析の際には、個々のデータの持つ個体差や外れ値があることを忘れてはいけませんが、そのランダム性に着目するならば、データは、[全体の平均] + [個体差] + [ノイズ] という形に分解できます。

この内、[個体差]と[ノイズ]はランダム要素を多分に含むものと言えるでしょう。

まず、得られたデータが表しているものを知るには、[全体の平均]を比較的正しく見積もれている必要があります。（見積もれていることを低バイアス、見積もりがずれていることを高バイアスと言います。）

その上でデータを分類するということは、そのデータの [個体差] を掴むこととほぼ同義です。すなわち、決定木（だけでなく学習モデル全般）は、ほぼデータの [個体差] を捉えるためにあります。

モデルはこの [個体差] をできる限り単純に表現するべきです。

なぜか。データのランダム要素は、[個体差] + [ノイズ] という形でほぼ書けますが、[個体差] を単純にすればするほど、それで表現しきれないデータの細かい部分は [ノイズ] に吸収されます。[個体差] が複雑であればその逆で、[ノイズ] はどんどん空っぽに近づきます。

[ノイズ] が空っぽに近づくということは、本来 [個体差] として処理してはいけないような部分も、[個体差] に含まれてしまいます。学習に用いる教師データ（=手元で取得できているデータ）には、必ずなんらかの偏りだったりノイズだったりがあり、これを全て [個体差] として処理すると、偏りのある悪いモデルになってしまいます。

ということで、[個体差] が複雑である、細かすぎる決定木も悪いモデルと言えるのです。（少し不正確ですが、[個体差] が複雑であることを高バリアンス、その逆を低バリアンスと言います。決定木は高バリアンスなモデルです。）

もちろんあまりにも単純すぎるモデルからは意義のある情報は何も得られませんが、複雑すぎるモデルにも価値はありません。

サンプルの少ない決定木は、そもそも全体の平均を上手く見積もれないのでポンコツ

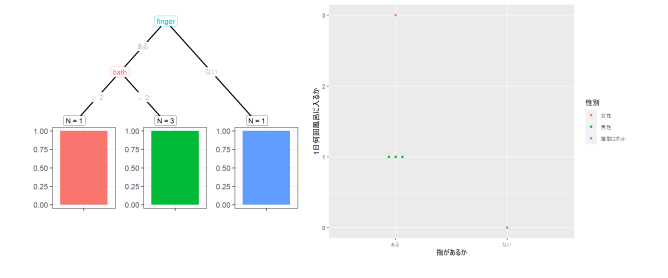
図4: 前回の記事で作成した3つ目の決定木。5人分のサンプルから、無謀にも、指の有無と1日の入浴回数で性別を分類する。

少ない教師データから作られた決定木は紛れもなくポンコツです。（じゃあどれくらいあればいいんだよというのはまた別の機会に）

データは、[全体の平均] + [個体差] + [ノイズ] という形に分解できると書きました。当然と思われるかもしれませんが、[全体の平均] と [個体差] が、「裏に隠れた法則をいい感じに言い当てられているか」というのは、サンプル数が増えれば増えるほど精度が上がります。

裏返せば、サンプル数が少ないと [全体の平均] と [個体差] の精度は下がります。サンプル数が少ない上に、更に外れ値を持つような変なサンプルが含まれていれば（この例で言えば猫型ロボット）、サンプル全体に占める変なサンプルの割合は上がってしまい、より外れ値に影響されやすいモデルができてしまいます。

この状態だと、いくらモデルを単純にしても [個体差] の影響は大きくなってしまいますが、そもそも [全体の平均] が全然上手く見積もれていないので、おおよそ使える学習器にはなりません。（高バイアス高バリアンスなモデルが出来上がります）

汎化性能で良し悪しを測る

ということで、前回の記事の2つ目（細かすぎ）と3つ目（サンプル少なすぎ）の決定木の問題点を説明しました。

両者とも教師データにはない未知のデータに対する分類が目的なのに、教師データに引っ張られすぎた悪い予測を出しやすいモデルになってしまっていました。

さて、「教師データにはない未知のデータに対する分類が目的」と書きましたが、未知の新しいデータに対して予測が当たる確率が高いことを汎化性能が良い（汎化誤差が小さい）と言います。

汎化の類義語は一般化、普遍化です。つまり汎化性能とは、教師データに限らない全てのデータに対する予測精度の高さを表します。

どれだけ手元の教師データに対する予測精度が高いモデルであろうと、汎化性能が悪ければ意味がありません。

ということで、前回の記事の2つ目（細かすぎ）と3つ目（サンプル少なすぎ）の決定木は汎化性能が悪いものの例でした。改めてそれぞれの汎化性能が悪い理由を整理します。

• 2つ目の決定木は、必要以上に深くすることで教師データに含まれるランダム性を、[個体差] に過度に含め過ぎてしまっていた。それが原因で教師データに特化し過ぎた融通の効かないモデルになってしまった。
• 3つ目の決定木は、教師データが少なすぎることで、浅い木であっても、そもそも [全体の平均] すら上手く見積もれていない上に、変なデータが、[個体差] に過度な影響を与えてしまっていた。

「教師データに特化し過ぎた融通の効かないモデル」と書きましたが、モデルをこういう風に学習させてしまうことを、過学習と言います。

決定木は深くすればするほど、より複雑なルールを表現できますが、やり過ぎるとその分教師データに引っ張られて過学習を起こし、汎化性能が悪くなってしまうというトレードオフがあります。

なので、1つ目の決定木のようなちょうどいい深さの決定木の方が、手元のデータにそぐわないことがあっても、汎化性能という観点で見れば、モデルとして優れていることになるのです。

実際に学習させるときには、汎化性能を測る指標が必要

さて、前回の記事で作った3つの決定木は、説明のために都合がいい上に、正直機械学習モデルなんてなくても目検で分類モデルを作れるような、そんなサンプルデータに基づいています。

しかし実際に機械学習を用いたいと思うような場面では、相手にするデータは当然もっと複雑で、モデルに使える特徴量も膨大で、そうしてできたモデルの良し悪し（=汎化性能）を評価する必要があります。

とてもではないですが、図3のようなものを見て「これはちょっとモデル複雑すぎるかもなぁ、、」とか「これじゃ使いもんにならんだろ」みたいなことはできないのです。

ということで実際にモデルを学習させた後は、汎化性能を測るための指標を用意し、その値を用いてモデルを評価します。

この指標は「これから来るであろう未知のデータ」を使ったものさしなので、厳密な値を測ることは不可能で、確率論を基にしたようなものを使います。（機械学習を行うためのパッケージでは恐らくデフォルトでこの指標の測り方が用意されているはずです。要件次第ではカスタマイズした方がより即したモデルが作れるはずです。）

ということで第3回はここで終わりです。この記事はこんな内容でした。

• データは、[全体の平均] + [個体差] + [ノイズ] という形に分解できる。
• 深すぎる決定木は、本来 [ノイズ] に含まれるべき情報が [個体差] に紛れ込み、過学習を起こしてしまう。（高バリアンス）
• 少ないデータから作られた決定木は、そもそも [全体の平均] が正しく見積もれない。（高バイアス）
• 汎化性能は、まだ見ぬ未知データに対する予測精度のことで、学習済みモデルの良し悪しを測るものさし。

次回は、決定木というモデルの致命的な弱点について説明し、それを克服する2つのモデル（GBDTとランダムフォレスト）を紹介します。